neural network embedded symmetry structure

In the language of the matrix, we know that a real symmetric matrix A=A^T has a lot of nice properties:

• All eigenvalues of a real symmetric matrix are real.
• Eigenvectors corresponding to distinct eigenvalues are orthogonal.
• A symmetric matrix can be written as, A=QΛQ^{-1}=QAQ^T where Q is an orthogonal matrix, and vice versa.
• Symmetric matrix A is positive definite if and only if all its eigenvalues are positive.
• etc …

Symmetric matrix also has a lot of applications in scientific areas, like Toeplitz matrix which is connected with convolution computation, and the very widely used Covariance matrix.which is critical for PCA (principal component analysis) and MDS (multidimensional scaling).

One of the main topics of this project is whether we could use a neural network to represent a symmetric matrix by multiplying A and A^T . The interesting part here is that under the assumption of the linear transformation, it’s not difficult to solve a symmetric matrix by eigendecomposition.  However, by adding non-linear layers we can achieve a wider representation ability by exploring in a larger space.

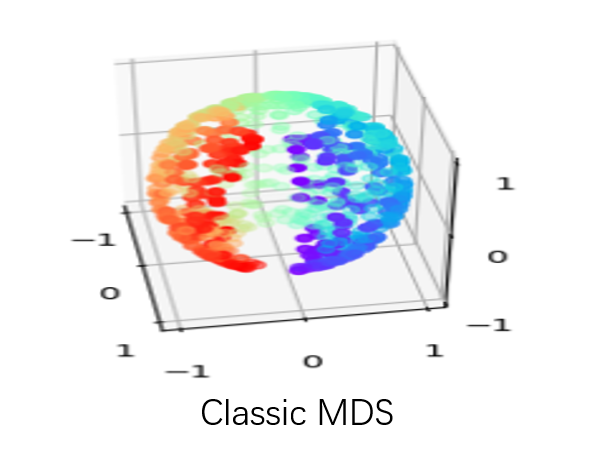
But here I want to show a very interesting result using a neural network to solving MDS problem which asks:  can we learn each point’s location by feeding in pairwise distance between them.

When we didn’t add non-linearity layers, our model can achieve the same results as classic MDS, however, to peek at the training process of the neural network what we found is amazing! The animation was shown how our model learns the embedding which tries to minimize the tension between pairwise distance which people would never think about before!

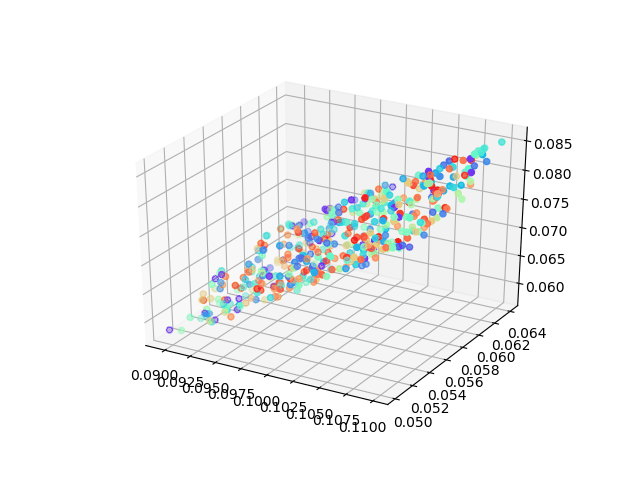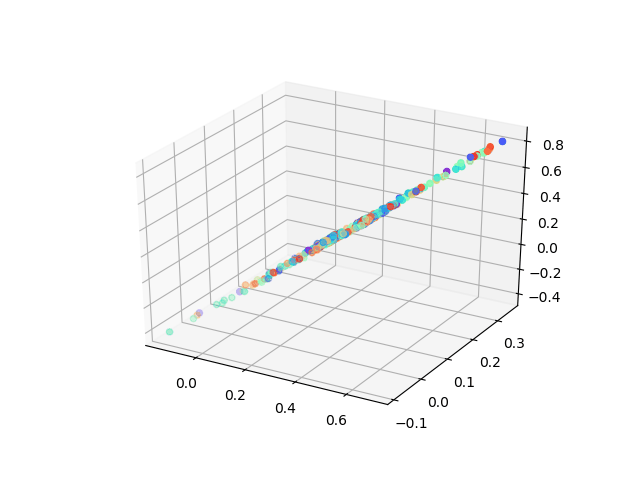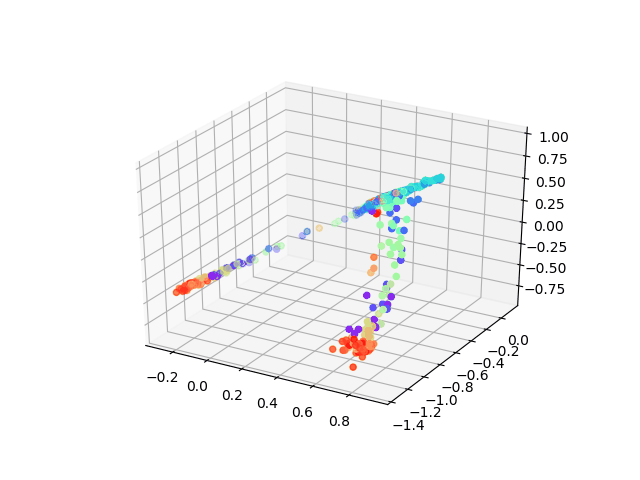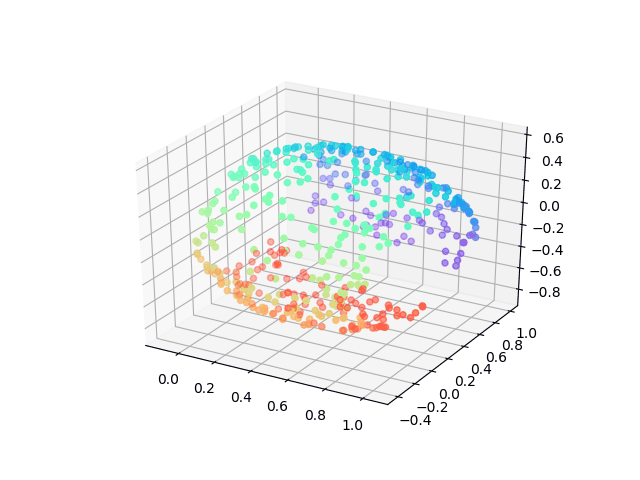
The advantages of this model could be:

• The model is scalable. Since we use batch training (which means only update the results by a small amount of input each time), we don’t have to compute the whole matrix’s inverse when we had thousands and millions of data points.
• We can easily insert any known embeddings of data points ( utilize prior knowledge )  by properly setting parameters updating in a network.
• We can add more non-linearity to fit for possible noise which we’re working on now :].